There is a very strong impulse for borrowers to take the shortest home loan fixed interest rate term at the moment. The demand for a fixed six month loan is the strongest it has ever been.
This is clearly because of the strong conviction mortgage interest rates are on the way down and borrowers will therefore get a lower rate in the future.
That is an understandable sentiment, but is it supported by the numbers?
Current fixed rates have a six month fixed at about 6.85% (carded/advertised), one year at 6.45%, and 18 months fixed at 5.99%.
So borrowers are betting that paying 6.85% now for six months, and either another six month term twice when that expires, or a 12 month term, will be better than taking the 5.99% rate now for 18 months fixed.
We can calculate where rates would need to fall to, to make that a "good bet".
Let's assume the mortgage taken out is $560,000 which is the July average of a new property purchase in the Reserve Bank C33 data series.
Over a six month term on a 30 year table-mortgage basis, you will pay interest of $18,983 (plus pay down your principal by $3,034) on monthly repayments of $3,669.
Over a fixed 18 month term on a 30 year table-mortgage basis, you will pay interest in those same six months of $16,593 (plus pay down your principal by $3,530) on monthly repayments of $3,354.
So the penalty for that first six months is that you will pay $315 more per month, a total of $1893, and owe $496 more on the loan at the end of six months.
You have decided to do that because you expect to make greater savings in the next period "because interest rates will have fallen by then".
So what do they need to fall by to achieve that?
If at the end of the six months you take out a one year fixed interest rate contract, that will need to be lower than 5.58% to justify the "pay-more-now-to pay-less-later" strategy.
The current one year fixed rate is 6.45%, so you are betting on fixed rates falling by about 90 basis points by the end of March 2025.
Essentially you are counting on four more Official Cash Rate rate cuts, AND counting on them not already being priced into the wholesale money rates that set the current rate offers.
You could be right.
At the time of writing, money markets are pricing in 100 basis points of cuts in that time period for this decision. (This is the ANZ pricing.)
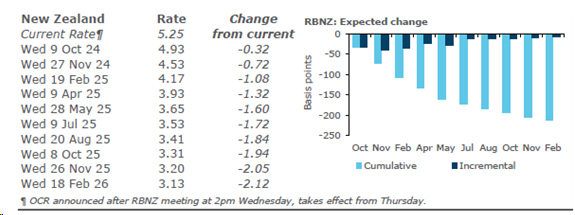
BUT, and it is a big 'but', this is the basis of current pricing that gives the 5.99% 18 month rate. IT COULD CHANGE, and probably will.
By choosing the higher six month rate now, everything must go as it is currently expected to make the March 2025 change a worthwhile decision now.
"Priced in" now means the expected four 25 basis points Reserve Bank rate cuts have to happen. If they do happen as currently expected, there will not be a further reductions from money market pressure to the current 18 month rate, although it might change due to competitive market-share pressures.
The risk is all weighted on those who choose the "pay-more-now-to pay-less-later" strategy.
It's the future, and no-one (but charlatans) know what is going to happen. Certainly banks don't dice with the future - they lay off their interest rate risk with hedging strategies.
But home loan borrowers are going into this without any hedging cover.
Because it is actually finely balanced, you should probably assess the risk of things not playing out as you currently 'expect'. Certainty about the future is a sure vulnerability in personal financial decision making. You need to balance a conviction you have with the acknowledgement of the downsides.
For those into the gritty details, here are the calculations used in this analysis.
Here is the base six-month situation:
| Borrow | $560,000 | |||||
| Rate | 6.85% | for six months | ||||
| term | 30 | yrs | ||||
| Start | Begin | payment | interest | principal | End | |
| 02-Sep-24 | -560,000.00 | -560,000.00 | ||||
| 1 | 02-Oct-24 | -560,000.00 | 3,669.45 | 3,152.88 | 516.57 | -559,483.43 |
| 2 | 02-Nov-24 | -559,483.43 | 3,669.45 | 3,254.97 | 414.48 | -559,068.95 |
| 3 | 02-Dec-24 | -559,068.95 | 3,669.45 | 3,147.63 | 521.82 | -558,547.13 |
| 4 | 02-Jan-25 | -558,547.13 | 3,669.45 | 3,249.52 | 419.93 | -558,127.20 |
| 5 | 02-Feb-25 | -558,127.20 | 3,669.45 | 3,247.08 | 422.37 | -557,704.83 |
| 6 | 02-Mar-25 | -557,704.83 | 3,669.45 | 2,930.62 | 738.83 | -556,966.00 |
Here is the subsequent 12 months that you need it to be to be no worse off than taking 18 months now:
| Borrow | $560,000 | |||||
| Rate | 5.58% | for twelve months | ||||
| term | 30 | yrs | ||||
| Start | Begin | payment | interest | principal | End | |
| 02-Mar-25 | ||||||
| 7 | 02-Apr-25 | -556,966.00 | 3,209.37 | 2,641.69 | 567.68 | -556,398.32 |
| 8 | 02-May-25 | -556,398.32 | 3,209.37 | 2,553.87 | 655.50 | -555,742.82 |
| 9 | 02-Jun-25 | -555,742.82 | 3,209.37 | 2,635.89 | 573.48 | -555,169.34 |
| 10 | 02-Jul-25 | -555,169.34 | 3,209.37 | 2,548.23 | 661.14 | -554,508.20 |
| 11 | 02-Aug-25 | -554,508.20 | 3,209.37 | 2,630.03 | 579.34 | -553,928.86 |
| 12 | 02-Sep-25 | -553,928.86 | 3,209.37 | 2,627.28 | 582.09 | -553,346.77 |
| 13 | 02-Oct-25 | -553,346.77 | 3,209.37 | 2,539.86 | 669.51 | -552,677.26 |
| 14 | 02-Nov-25 | -552,677.26 | 3,209.37 | 2,621.35 | 588.02 | -552,089.24 |
| 15 | 02-Dec-25 | -552,089.24 | 3,209.37 | 2,534.09 | 675.28 | -551,413.96 |
| 16 | 02-Jan-26 | -551,413.96 | 3,209.37 | 2,615.36 | 594.01 | -550,819.95 |
| 17 | 02-Feb-26 | -550,819.95 | 3,209.37 | 2,612.54 | 596.83 | -550,223.12 |
| 18 | 02-Mar-26 | -550,223.12 | 3,209.37 | 2,357.16 | 852.21 | -549,370.91 |
And here is the 18 month now situation as the 'certainty' base:
| Borrow | $560,000 | |||||
| Rate | 5.99% | for 18 months | ||||
| term | 30 | yrs | ||||
| Start | Begin | payment | interest | principal | End | |
| 02-Sep-24 | -560,000.00 | -560,000.00 | ||||
| 1 | 02-Oct-24 | -560,000.00 | 3,353.88 | 2,757.04 | 596.84 | -559,403.16 |
| 2 | 02-Nov-24 | -559,403.16 | 3,353.88 | 2,845.91 | 507.97 | -558,895.19 |
| 3 | 02-Dec-24 | -558,895.19 | 3,353.88 | 2,751.60 | 602.28 | -558,292.91 |
| 4 | 02-Jan-25 | -558,292.91 | 3,353.88 | 2,840.26 | 513.62 | -557,779.29 |
| 5 | 02-Feb-25 | -557,779.29 | 3,353.88 | 2,837.64 | 516.24 | -557,263.05 |
| 6 | 02-Mar-25 | -557,263.05 | 3,353.88 | 2,560.66 | 793.22 | -556,469.83 |
| 7 | 02-Apr-25 | -556,469.83 | 3,353.88 | 2,830.98 | 522.90 | -555,946.93 |
| 8 | 02-May-25 | -555,946.93 | 3,353.88 | 2,737.09 | 616.79 | -555,330.14 |
| 9 | 02-Jun-25 | -555,330.14 | 3,353.88 | 2,825.19 | 528.69 | -554,801.45 |
| 10 | 02-Jul-25 | -554,801.45 | 3,353.88 | 2,731.45 | 622.43 | -554,179.02 |
| 11 | 02-Aug-25 | -554,179.02 | 3,353.88 | 2,819.33 | 534.55 | -553,644.47 |
| 12 | 02-Sep-25 | -553,644.47 | 3,353.88 | 2,816.61 | 537.27 | -553,107.20 |
| 13 | 02-Oct-25 | -553,107.20 | 3,353.88 | 2,723.11 | 630.77 | -552,476.43 |
| 14 | 02-Nov-25 | -552,476.43 | 3,353.88 | 2,810.67 | 543.21 | -551,933.22 |
| 15 | 02-Dec-25 | -551,933.22 | 3,353.88 | 2,717.33 | 636.55 | -551,296.67 |
| 16 | 02-Jan-26 | -551,296.67 | 3,353.88 | 2,804.67 | 549.21 | -550,747.46 |
| 17 | 02-Feb-26 | -550,747.46 | 3,353.88 | 2,801.87 | 552.01 | -550,195.45 |
| 18 | 02-Mar-26 | -550,195.45 | 3,353.88 | 2,528.19 | 825.69 | -549,369.76 |
Obviously there are may ways to look at this issue, and this is just one.
The choice we laid out here is not the only one, even if it is the one many seem to be making.
16 Comments
David, Could calculate.co.nz put one of these together for interest.co.nz?
It's a common query - a "what-if" - that all mortgage holders face.
And it is a much more frequent query than the "how much can I borrow" query. And one that really shouldn't be left to a 'reckons'.
And it would cut down on the irritating 'reckons' we see so much of in the comments from those that don't use spreadsheets.
Thoughts?
Hey...It is very easy DIY using your favorite AI tool...
For e.g. Log into https://gemini.google.com/?hl=en, copy and paste the below prompt with your own values.
You will get the answer in a split second...I just tested it for my own mortgage that is going to be renewed.
Mortgage Interest Rate What-If Analysis Calculation
Scenario:
* Original Principal: [Your original loan amount]
* Current Date: [Today's date in YYYY-MM-DD format]
* Loan End Date: [The date your loan is scheduled to be fully paid off in YYYY-MM-DD format]
* Option 1 (Short-Term Rate):
* Interest Rate: [The offered short-term interest rate]
* Term: [The term of the short-term rate in months]
* Option 2 (Long-Term Rate):
* Interest Rate: [The offered long-term interest rate]
* Term: [The term of the long-term rate in months]
Assumptions:
* Interest Calculation: Daily
* Principal Payments: Monthly
Task:
1. Calculate the monthly payment amount based on the original principal, long-term interest rate, and loan end date.
2. For both the short-term and long-term options, calculate the daily interest and remaining principal after each monthly payment for their respective terms.
3. Determine the total interest paid for each option over their respective terms.
4. Calculate the break-even interest rate needed for the short-term option after its term expires to result in the same total interest paid over the long-term period as the long-term option.
5. Present the break-even interest rate as a percentage, along with a clear statement explaining its significance in the context of the mortgage decision.
Additional Notes:
* Ensure calculations are accurate and handle daily interest and monthly payments correctly.
* Double-check results and compare with other reliable sources if necessary.
* Emphasize that this is an estimate based on the provided assumptions and should not be considered financial advice.
AND you have to be certain that the banks would pass all of those rate cuts in full on to the customer, instead of increasing their NIMs. Currently the banks and money markets are front running the RBNZ so its quite likely that down the track the banks will only start passing on portions of any rate cuts rather than the full amount.
I noticed you used a table mortgage to do these calculations.
Table mortgages 'front load' interest payments. They enable a more affordable payment schedule calculated over a longer term. (i.e. the interest front-loaded is calculated based on the loan term, not the interest rate period)
Are table mortgages a form of 'lock-in' for banks? A more attractive fixed mortgage rate but due to front-loading only effective if the full term is completed.
If a customer shifts banks at the end of a fixed-term rate period, don't they effectively start again? Due to the front loading isn't the effective interest rate higher than the published rate ?
Table mortgages are used to lock in the interest rate for the entire amortisation term. (30 years in the US). In NZ that's not available.
The alternative approaches are penalised with a higher interest rate. (floating, variable, offset etc). So financially the outcome (the total cost of the loan after it is paid off) might be similar. If additional principal payments are made then of course the total interest can be much less.
While they are the dominant form of lending, and they get first home buyers into the market, are they good for borrowers and the economy?
You can test what you're saying using this calculator https://www.interest.co.nz/calculators/full-function-mortgage-calculator
It's already too late for this strategy, if you did fix short 6m as little as 6 weeks ago you can save that money now by breaking your mortgage even with you current bank and paying the break fee to move to the 18m rate that has no risk further out. If they drop faster then just change banks...
We welcome your comments below. If you are not already registered, please register to comment.
Remember we welcome robust, respectful and insightful debate. We don't welcome abusive or defamatory comments and will de-register those repeatedly making such comments. Our current comment policy is here.